Scientific explanation on Bondarev's lifting Air Screw Blade

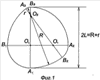
The geometric characteristics of the air screw include: the shape of the blades in plan view, the shape of the blade profile, the diameter, the angle of inclination of the blade and the geometric pitch of the screw.

According to the shape of the blade in plan view the screws can be very diverse.

The blades of the lifting air screw are the most responsible and loaded units of an aircraft, providing the creation of required lift. It must meet diverse and controversial requirements, such as:

• ensuring the requirements of static strength: the stresses acting in the blade spar from centrifugal forces in flight and from mass forces in the parking lot shall not exceed the permissible stresses;
• providing the necessary stock at flutter;
• no resonance oscillations;
• providing the necessary resource;
• ensuring sufficient stiffness of the blade on the bend in in-planes of traction and rotation, as well as torsion;
• obtaining high aerodynamic qualities;
• providing low (by resource) cost and technological effectiveness.

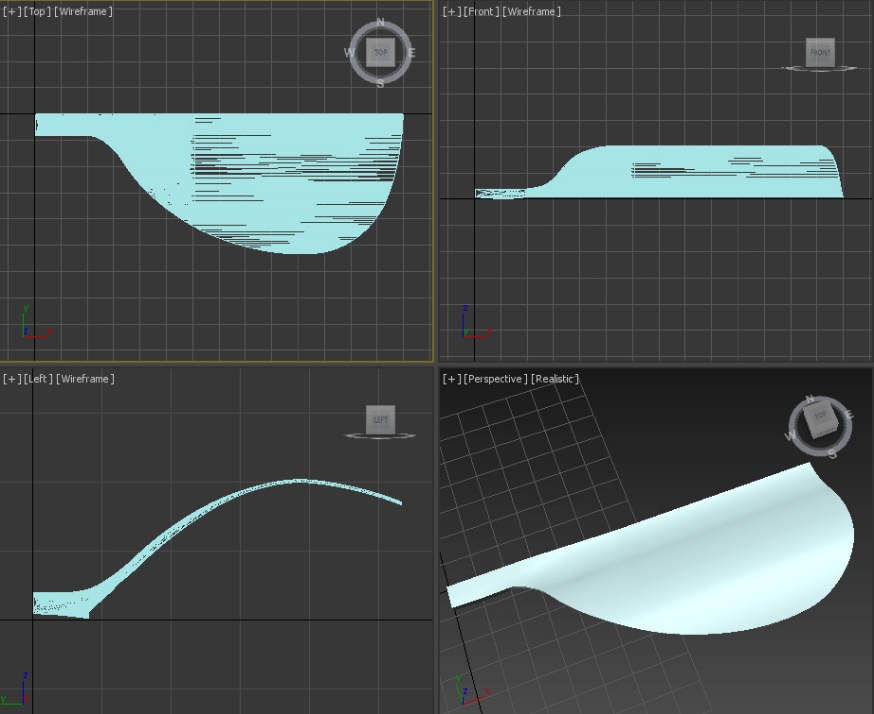
The blade developed according to specified requirements allowed to create a screw of new design.

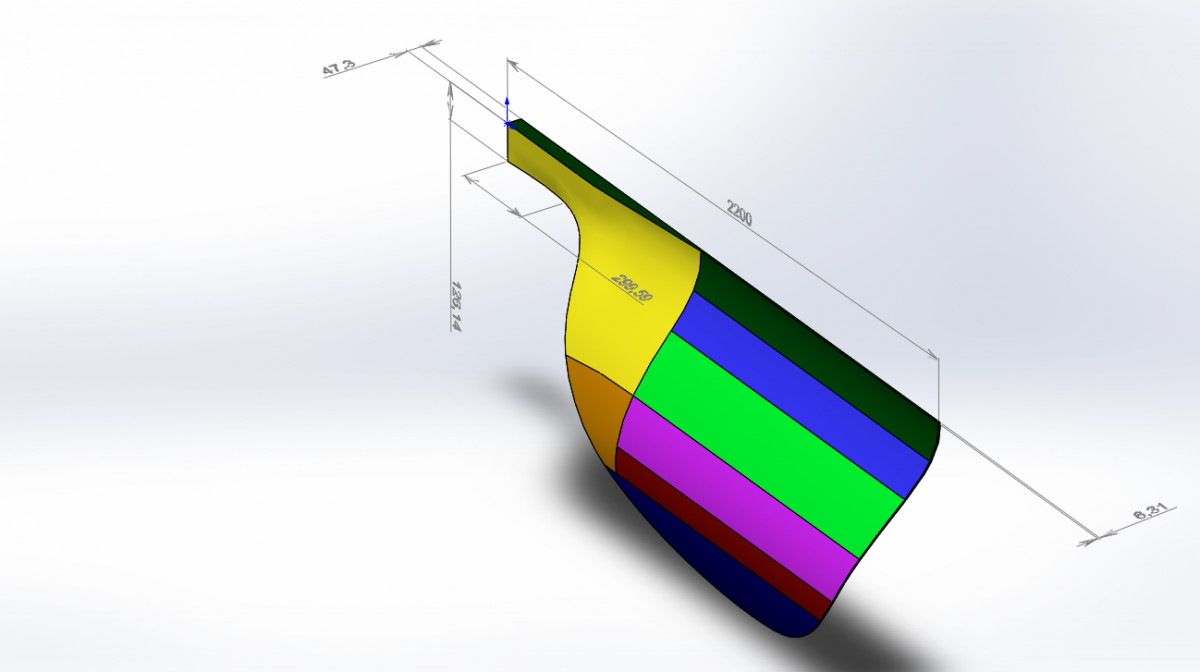
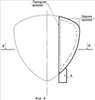
 The aerodynamic screw with blades and roots fixed on the axis of the screw, the root is made unified for all blades and the blades of the aerodynamic screw are made with periphery of feather, defined along the line of the curve of equal width.

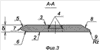
The invention refers to blades of air screws used in aviation and wind power engineering. The air screw blade contains a root and a feather. The blade feather is made of parent sheet with parallel internal and external surfaces. The perimeter of the blade feather is made at a curve of equal (constant) width. The front lead-in rim has chamfers from the side of the surfaces and a radius in the middle of the rim. The rear rim of the blade is made with chamfering around the perimeter from the outside surface and the radius facing the inner surface. The feather of the air screw blade can be performed by dividing the curve of equal width if there is a straight front rim with the corresponding elements and the back rim with chamfering. The blade feather can be trimmed to reduce the size of the blade along the line, parallel to the curve of equal width, with both the front rim and the back rim, and butt of the blade feather.

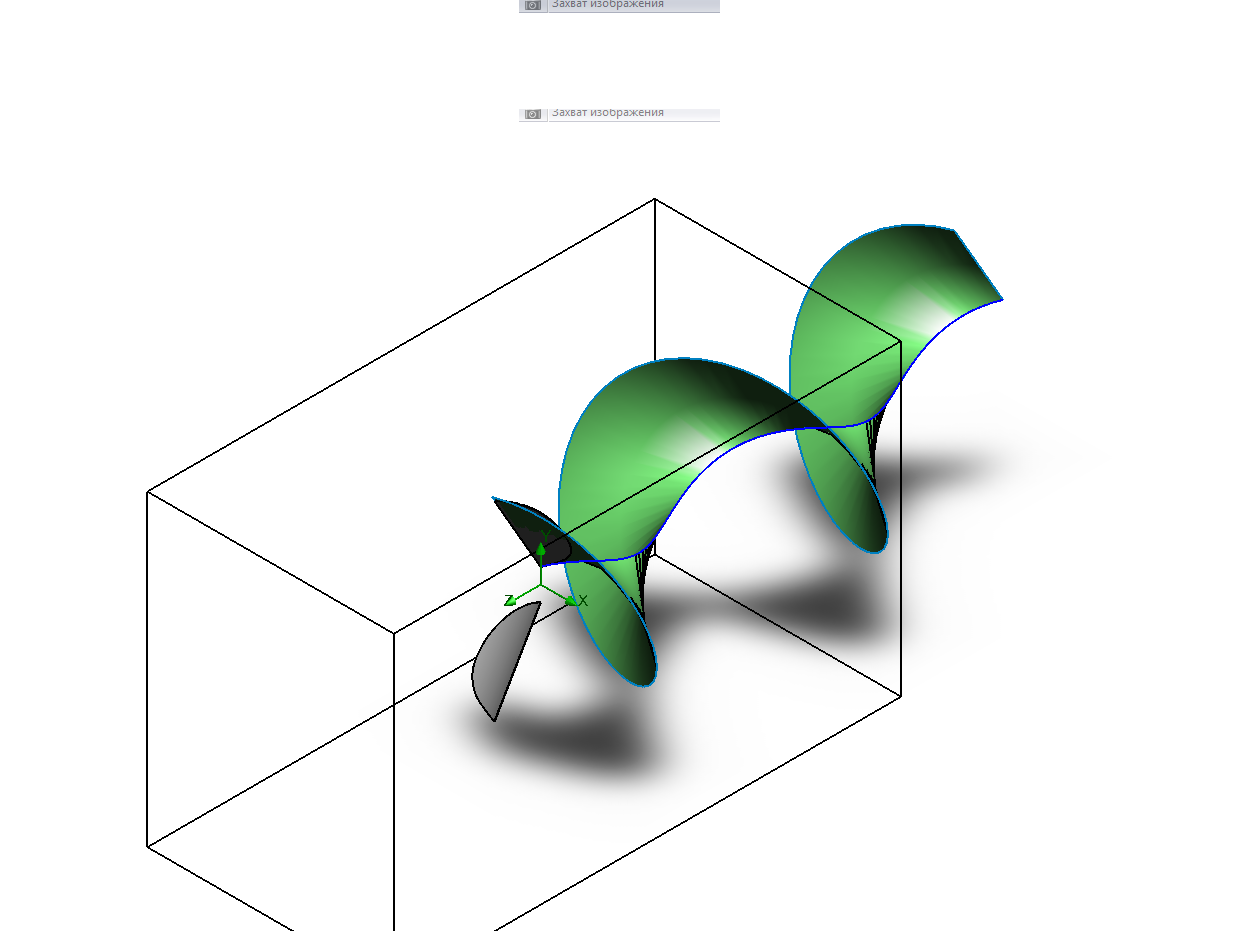
The feather of the air screw blade can be bent relative to the rotation plane around the cylinder, the radius of which is determined by the dependence of 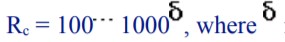is the thickness of the sheet.

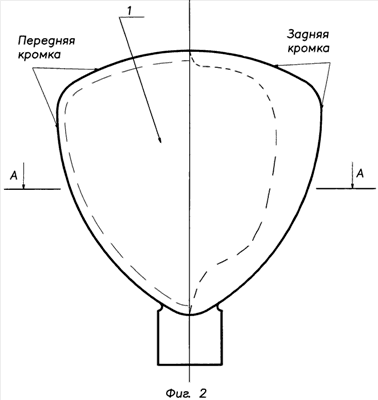
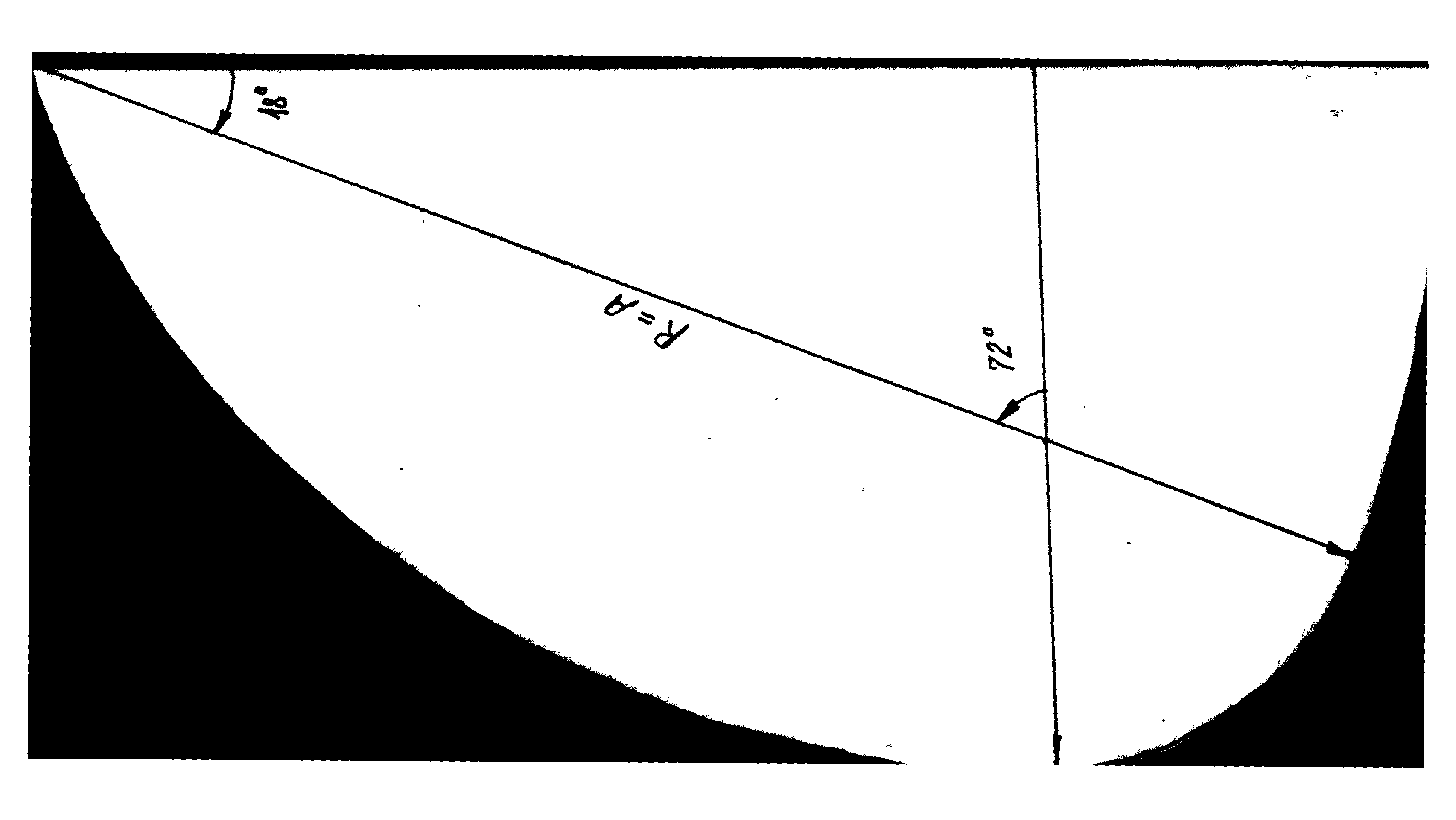
The study of the geometry of the created screw revealed its complete coincidence with the Golden Triangle.

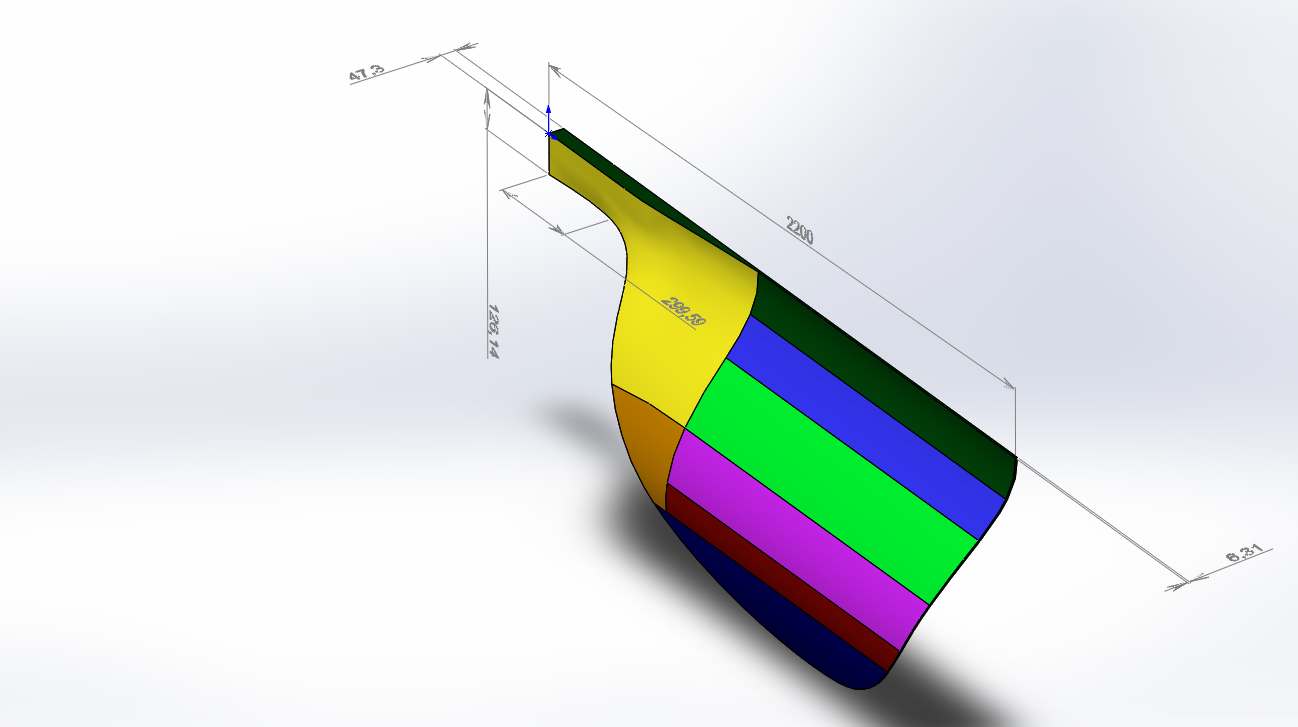
Bondarev's air screw blade

The Golden Triangle is an isosceles triangle that has a lateral length ratio to the length of the base equal to the Phidias number. One of its properties is that, the bisectrix lengths of its angles at the base are equal to the length of the base. The remaining properties are derived from the pentagram properties.

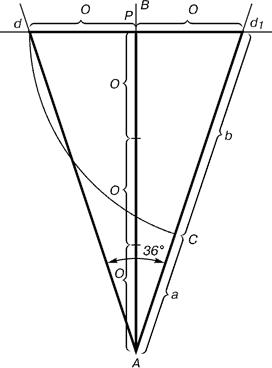
The sides of the Golden Triangle form an angle of 36° at the top, and the base, deferred on the lateral side, divides it into the proportions of the Golden Section.

One of the properties of the Golden Triangle is that, the bisectrix lengths of its angles at the base are equal to the length of the base. The remaining properties are derived from the pentagram properties, which we will look at later.

One of the properties of the Golden Triangle is that, the bisectrix lengths of its angles at the base are equal to the length of the base. The remaining properties are derived from the pentagram properties, which we will look at later.

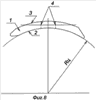
Building of a Golden Triangle

We construct a right line AB. From point A we three times mark off the interval O of arbitrary size, through the received point P we construct a perpendicular to the line AB, on the perpendicular to the right and to the left from the point P we construct segments intervals O. The received points d and d1 we connect by right lines with the point A. The interval dd1 we mark off on the line Ad1, receiving point C. The point C has divided the line Ad1 in proportion of the Golden Section.

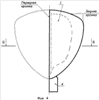
There are simple generalizations of the geometrical design of a blade. The figure of a constant diameter can be constructed by taking as basis a star with sides of the same length, not necessarily a regular.

You can also build the figure by starting with an arbitrary triangle; at the same time each vertex is the center of not one, but two arcs, because of that the angles are smoothed (Let the angle A be the smallest of the triangle ABC (and thus the opposite side a is the shortest). Let's select a non-negative radius r_A. Now we need to sort out the radius r_B and r_С so, that it fulfills the formula a+r_В+r_С=r_A+b+r_С=r_A+r_В+c. This is easy to do, the diameter of the figure will be equal 2r_A+b+с–a. The smallest radius adjusts the smoothness at the corners: at r_A=0 we receive a figure with one sharp angle, at r_A→∞ a figure that turns into a circle.

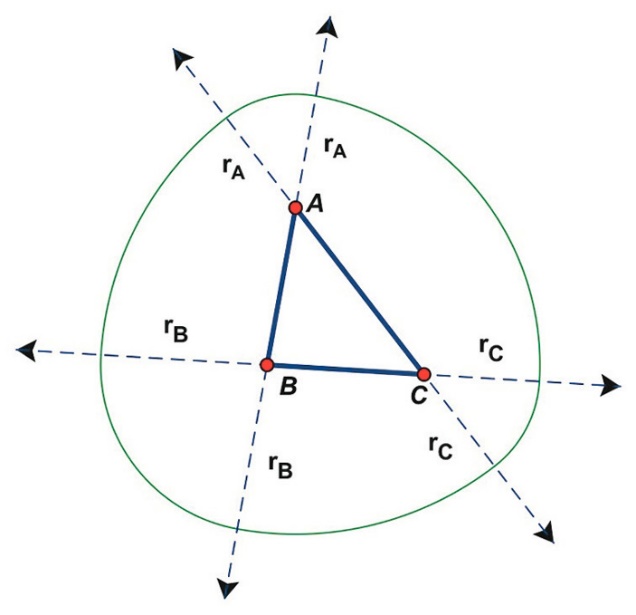
The Golden Triangle of constant diameter with smoothed corners

The Göttingen laboratory in Germany conducted in the beginning of the last century a very widespread investigation on curved aerofoils reminding on wings of birds. The data on one of the aerofoils formed the basis of this blade. With reduction of the Reynolds number the frontal resistance increases and aerodynamic efficiency falls.

The advantage of riffles is as well that they can work successfully at small Reynolds numbers, which is typical for small amateur windmills. The flat plate works on Reynolds numbers even smaller than the rifles, but inability to build on flat profiles fast-speed wind mills decreases the speed of rotation.

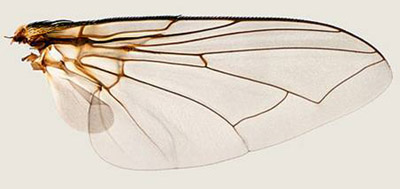
Examples of use of the geometry of the Golden Triangle in nature

1. Winged maple seeds — ash-key consisting of two halves — seeds with wings, each of which is 2-2.5 cm long. The ash-key sits on a long leafstalk.

2. The wing of an insect

3. Minerals

Developments of screws closest to the design of the Bondarev screw

New wind turbine (Australia): has 10 times more blades than a traditional one. Working with the slow wind, it does not give much noise or vibration, and thus produces 30% more energy than windmills-competitors.

The wind generator with the diameter of 6.5 meters endowed by 30 aluminum blades in form of riffles.

The Wind Lens (Japan): Consists of an input propeller shrouding, diffuser and outer edge. The strong vortex-type flow generated by the diffuser and the outer edge of the wind lens form a low-pressure area outside of the turbine. This increases the pressure difference, which allows to send more wind into the wind lens. More air gives more energy. The researchers say that this method is able to increase the power produced by the wind turbine, while reducing the noise.

Copyright Fulmina Foundation

Powered by Froala Editor